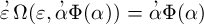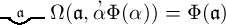§ 10. Dadurch, dass wir die
Zeichenverbindung 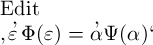 als gleichbedeutend mit
als gleichbedeutend mit 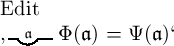 hingestellt haben, ist freilich die Bedeutung eines Namens wie
hingestellt haben, ist freilich die Bedeutung eines Namens wie
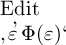 noch
keineswegs vollständig festgestellt. Wir haben nur ein Mittel,
einen Werthverlauf immer wiederzuerkennen, wenn er durch einen
Namen wie
noch
keineswegs vollständig festgestellt. Wir haben nur ein Mittel,
einen Werthverlauf immer wiederzuerkennen, wenn er durch einen
Namen wie 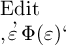 bezeichnet ist, durch welchen er schon als Werthverlauf erkennbar
ist. Aber weder können wir bis jetzt entscheiden, ob ein
Gegenstand, der uns nicht als solcher gegeben ist, ein
Werthverlauf sei, und welcher Function er etwa zugehöre, noch
können wir im Allgemeinen entscheiden, ob ein gegebener
Werthverlauf eine gegebene Eigenschaft habe, wenn wir nicht
wissen, dass diese Eigenschaft verbunden sei mit einer
Eigenschaft der zugehörigen Function. Nehmen wir an, es sei
eine Function, welche niemals denselben Werth für
verschiedene Argumente erhält, so gilt für die Gegenstände, deren
Namen die Form
bezeichnet ist, durch welchen er schon als Werthverlauf erkennbar
ist. Aber weder können wir bis jetzt entscheiden, ob ein
Gegenstand, der uns nicht als solcher gegeben ist, ein
Werthverlauf sei, und welcher Function er etwa zugehöre, noch
können wir im Allgemeinen entscheiden, ob ein gegebener
Werthverlauf eine gegebene Eigenschaft habe, wenn wir nicht
wissen, dass diese Eigenschaft verbunden sei mit einer
Eigenschaft der zugehörigen Function. Nehmen wir an, es sei
eine Function, welche niemals denselben Werth für
verschiedene Argumente erhält, so gilt für die Gegenstände, deren
Namen die Form 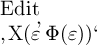 haben, ganz dasselbe Kennzeichen zur Wiedererkennung wie für die
Gegenstände, deren Zeichen die Form
haben, ganz dasselbe Kennzeichen zur Wiedererkennung wie für die
Gegenstände, deren Zeichen die Form 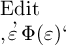 haben. Es ist dann nämlich auch
haben. Es ist dann nämlich auch 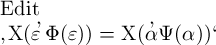 gleichbedeutend mit
gleichbedeutend mit 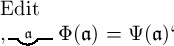 .
Hieraus geht hervor, dass durch die Gleichsetzung der Bedeutung
von
.
Hieraus geht hervor, dass durch die Gleichsetzung der Bedeutung
von 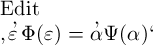 mit
der von
mit
der von 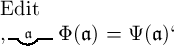 die Bedeutung eines Namens wie
die Bedeutung eines Namens wie 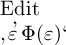 keineswegs völlig bestimmt ist, wenigstens, wenn es eine solche
Function Χ(ξ) giebt, deren Werth
für einen Werthverlauf als Argument diesem selbst nicht immer
gleich ist. Wie wird nun diese Unbestimmtheit aufgehoben?
Dadurch, dass für jede Function bei ihrer Einführung bestimmt
wird, welche Werthe sie für Werthverläufe als Argumente erhält,
ebenso wie für alle andern Argumente. Thun wir dies für die
bisher betrachteten Functionen! Es sind folgende:
Die letzte kann ausser Betracht bleiben, da als ihr
Argument immer ein Wahrheitswerth betrachtet werden kann. Es
macht ja bei ihr keinen Unterschied, ob man als Argument einen
Gegenstand nimmt oder den Werth, den die Function —ξ für diesen Gegenstand als Argument hat. Wir
können nun noch die Function —ξ auf
die Function ξ=ζ zurückführen. Nach unsern
Festsetzungen hat nämlich die Function ξ=(ξ=ξ) für jedes Argument denselben Werth
wie die Function —ξ; denn der Werth
der Function ξ=ξ ist für jedes Argument das Wahre.
Daraus folgt, dass
keineswegs völlig bestimmt ist, wenigstens, wenn es eine solche
Function Χ(ξ) giebt, deren Werth
für einen Werthverlauf als Argument diesem selbst nicht immer
gleich ist. Wie wird nun diese Unbestimmtheit aufgehoben?
Dadurch, dass für jede Function bei ihrer Einführung bestimmt
wird, welche Werthe sie für Werthverläufe als Argumente erhält,
ebenso wie für alle andern Argumente. Thun wir dies für die
bisher betrachteten Functionen! Es sind folgende:
Die letzte kann ausser Betracht bleiben, da als ihr
Argument immer ein Wahrheitswerth betrachtet werden kann. Es
macht ja bei ihr keinen Unterschied, ob man als Argument einen
Gegenstand nimmt oder den Werth, den die Function —ξ für diesen Gegenstand als Argument hat. Wir
können nun noch die Function —ξ auf
die Function ξ=ζ zurückführen. Nach unsern
Festsetzungen hat nämlich die Function ξ=(ξ=ξ) für jedes Argument denselben Werth
wie die Function —ξ; denn der Werth
der Function ξ=ξ ist für jedes Argument das Wahre.
Daraus folgt, dass
Seite
17
der Werth der Function ξ=(ξ=ξ) nur
für das Wahre als Argument das Wahre ist, und dass er für alle
andern Argumente das Falsche ist, grade wie bei der Function
—ξ. Nachdem so Alles auf die
Betrachtung der Function ξ=ζ zurückgeführt ist, fragen wir, welche
Werthe diese habe, wenn ein Werthverlauf als Argument auftritt.
Da wir bisher nur die Wahrheitswerthe und Werthverläufe als
Gegenstände eingeführt haben, so kann es sich nur darum handeln,
ob einer der Wahrheitswerthe etwa ein Werthverlauf sei. Wenn das
nicht der Fall ist, so ist damit auch entschieden, dass der Werth
der Function ξ=ζ immer das Falsche ist, wenn als eins
ihrer Argumente ein Wahrheitswerth und als anderes ein
Werthverlauf genommen wird. Wenn andrerseits das Wahre zugleich
der Werthverlauf der Function Φ(ξ)
ist, so ist damit auch entschieden, was der Werth der Function
ξ=ζ
in allen Fällen ist, wo als eins der Argumente das Wahre genommen
wird, und ähnlich so verhält es sich, wenn das Falsche zugleich
der Werthverlauf einer gewissen Function ist. Die Frage nun, ob
einer der Wahrheitswerthe ein Werthverlauf sei, kann unmöglich
daraus entschieden werden, dass 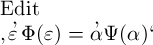 dieselbe Bedeutung haben soll wie
dieselbe Bedeutung haben soll wie 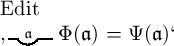 . Es
ist möglich, allgemein festzusetzen, dass
. Es
ist möglich, allgemein festzusetzen, dass 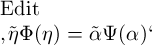 dasselbe bedeuten solle wie
dasselbe bedeuten solle wie 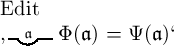 ,
ohne dass daraus die Gleichheit von
,
ohne dass daraus die Gleichheit von 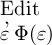 und
und
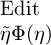 erschlossen werden kann. Wir hätten dann etwa eine Klasse von
Gegenständen, die Namen von der Form
erschlossen werden kann. Wir hätten dann etwa eine Klasse von
Gegenständen, die Namen von der Form 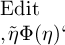 hätten und für deren Unterscheidung und Wiedererkennung dasselbe
Kennzeichen gälte wie für die Werthverläufe. Wir könnten nun die
Function Χ(ξ) dadurch bestimmen,
dass wir sagten, ihr Werth solle das Wahre sein für
hätten und für deren Unterscheidung und Wiedererkennung dasselbe
Kennzeichen gälte wie für die Werthverläufe. Wir könnten nun die
Function Χ(ξ) dadurch bestimmen,
dass wir sagten, ihr Werth solle das Wahre sein für 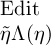 als
Argument und er solle
als
Argument und er solle 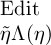 sein für das Wahre als Argument; der Werth der Function
Χ(ξ) solle ferner das Falsche sein
für das Argument
sein für das Wahre als Argument; der Werth der Function
Χ(ξ) solle ferner das Falsche sein
für das Argument 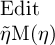 und er solle
und er solle 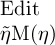 sein für das Falsche als Argument; für jedes andere Argument
solle der Werth der Function Χ(ξ)
Korrektur innerhalb des
Formelteils: funcarg [Rev.: thiel] mit diesem
selbst zusammenfallen. Wenn nun die Functionen Λ(ξ) und Μ(ξ)
nicht immer für dasselbe Argument denselben Werth haben, so hat
unsere Function Χ(ξ) für
verschiedene Argumente nie denselben Werth, und daher ist dann
auch
sein für das Falsche als Argument; für jedes andere Argument
solle der Werth der Function Χ(ξ)
Korrektur innerhalb des
Formelteils: funcarg [Rev.: thiel] mit diesem
selbst zusammenfallen. Wenn nun die Functionen Λ(ξ) und Μ(ξ)
nicht immer für dasselbe Argument denselben Werth haben, so hat
unsere Function Χ(ξ) für
verschiedene Argumente nie denselben Werth, und daher ist dann
auch 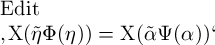 immer gleichbedeutend mit
immer gleichbedeutend mit 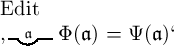 .
Die Gegenstände, deren Namen die Form
.
Die Gegenstände, deren Namen die Form 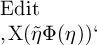 hätten, würden dann also durch dasselbe Mittel wiedererkannt wie
die Werthverläufe, und es wäre
hätten, würden dann also durch dasselbe Mittel wiedererkannt wie
die Werthverläufe, und es wäre 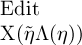 das Wahre und
das Wahre und 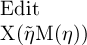 das Falsche. Ohne also mit der Gleichsetzung von
das Falsche. Ohne also mit der Gleichsetzung von 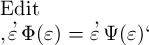 mit
mit
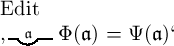 in
Widerspruch zu gerathen, ist es immer möglich zu bestimmen, dass
ein beliebiger Werthverlauf das Wahre und ein beliebiger anderer
das Falsche sein solle. Setzen wir demnach fest, dass
in
Widerspruch zu gerathen, ist es immer möglich zu bestimmen, dass
ein beliebiger Werthverlauf das Wahre und ein beliebiger anderer
das Falsche sein solle. Setzen wir demnach fest, dass
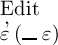 das
Wahre und dass
das
Wahre und dass  das Falsche sein solle!
das Falsche sein solle! 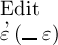 ist der Werthverlauf der Function —ξ, deren Werth nur dann das Wahre ist, wenn
das Argument das Wahre ist, und deren Werth für alle andern
Argumente das Falsche ist. Alle Functionen, von denen dies gilt,
haben
ist der Werthverlauf der Function —ξ, deren Werth nur dann das Wahre ist, wenn
das Argument das Wahre ist, und deren Werth für alle andern
Argumente das Falsche ist. Alle Functionen, von denen dies gilt,
haben
Seite
18
denselben Werthverlauf und dieser ist nach unserer Festsetzung
das Wahre. Demnach ist 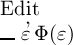 nur dann das Wahre, wenn die Function Φ(ξ) ein Begriff ist, unter den nur das Wahre
fällt; in allen andern Fällen ist
nur dann das Wahre, wenn die Function Φ(ξ) ein Begriff ist, unter den nur das Wahre
fällt; in allen andern Fällen ist 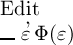 das
Falsche. Ferner ist
das
Falsche. Ferner ist  der Werthverlauf der Function
der Werthverlauf der Function  ,
deren Werth nur dann das Wahre ist, wenn das Argument das Falsche
ist, und deren Werth für alle andern Argumente das Falsche ist.
Alle Functionen, von denen dies gilt, haben denselben
Werthverlauf, und dieser ist nach unserer Festsetzung das
Falsche. Jeder Begriff also, unter den das Falsche und nur dieses
fällt, hat als Begriffsumfang das Falsche. Wir
haben hiermit die Werthverläufe so
weit bestimmt, als es hier möglich ist. Erst wenn es sich ferner
darum handeln sollte, eine Function einzuführen, welche auf die
bisher bekannten Functionen nicht ganz zurückführbar ist, können
wir festsetzen, welche Werthe sie für Werthverläufe als Argumente
haben solle; und dies kann dann ebenso wohl als eine Bestimmung
der Werthverläufe wie jener Function angesehen werden.
,
deren Werth nur dann das Wahre ist, wenn das Argument das Falsche
ist, und deren Werth für alle andern Argumente das Falsche ist.
Alle Functionen, von denen dies gilt, haben denselben
Werthverlauf, und dieser ist nach unserer Festsetzung das
Falsche. Jeder Begriff also, unter den das Falsche und nur dieses
fällt, hat als Begriffsumfang das Falsche. Wir
haben hiermit die Werthverläufe so
weit bestimmt, als es hier möglich ist. Erst wenn es sich ferner
darum handeln sollte, eine Function einzuführen, welche auf die
bisher bekannten Functionen nicht ganz zurückführbar ist, können
wir festsetzen, welche Werthe sie für Werthverläufe als Argumente
haben solle; und dies kann dann ebenso wohl als eine Bestimmung
der Werthverläufe wie jener Function angesehen werden.
1 Damit ist nicht gesagt, dass der Sinn
derselbe sei.
1 Es liegt nahe, unsere Festsetzung so
zu verallgemeinern, dass jeder Gegenstand als Werthverlauf
aufgefasst werde, nämlich als Umfang eines Begriffes, unter den
er als einziger Gegenstand fällt Ein Begriff, unter den der
Gegenstand Δ als einziger fällt,
ist Δ=ξ. Wir versuchen die Festsetzung: es
sei 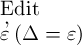 dasselbe wie Δ. Eine solche ist für
jeden Gegenstand möglich, der uns unabhängig von Werthverläufen
gegeben ist, aus demselben Grunde, den wir bei den
Wahrheitswerthen gesehen haben. Aber ehe wir diese Festsetzung
allgemein machen dürfen, fragt es sich, ob sie nicht in
Widerspruch mit unserm Wiedererkennungszeichen der Werthverläufe
stehe, wenn wir für Δ einen
Gegenstand nehmen, der uns schon als Werthverlauf gegeben ist. Es
geht nämlich nicht an, sie nur für solche Gegenstände gelten zu
lassen, welche uns nicht als Werthverläufe gegeben sind, weil die
Weise wie ein Gegenstand gegeben ist, nicht als dessen
unveränderliche Eigenschaft angesehen werden darf, sintemal
derselbe Gegenstand in verschiedener Weise gegeben werden kann.
Setzen wir also für ‚Δ‘
dasselbe wie Δ. Eine solche ist für
jeden Gegenstand möglich, der uns unabhängig von Werthverläufen
gegeben ist, aus demselben Grunde, den wir bei den
Wahrheitswerthen gesehen haben. Aber ehe wir diese Festsetzung
allgemein machen dürfen, fragt es sich, ob sie nicht in
Widerspruch mit unserm Wiedererkennungszeichen der Werthverläufe
stehe, wenn wir für Δ einen
Gegenstand nehmen, der uns schon als Werthverlauf gegeben ist. Es
geht nämlich nicht an, sie nur für solche Gegenstände gelten zu
lassen, welche uns nicht als Werthverläufe gegeben sind, weil die
Weise wie ein Gegenstand gegeben ist, nicht als dessen
unveränderliche Eigenschaft angesehen werden darf, sintemal
derselbe Gegenstand in verschiedener Weise gegeben werden kann.
Setzen wir also für ‚Δ‘
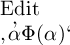 ein,
so erhalten wir
ein,
so erhalten wir 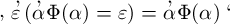
 und dies wäre gleichbedeutend mit
und dies wäre gleichbedeutend mit
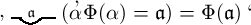
 was aber nur dann das Wahre bedeutet, wenn
Φ(ξ) ein Begriff ist, unter den nur
ein einziger Gegenstand, nämlich
was aber nur dann das Wahre bedeutet, wenn
Φ(ξ) ein Begriff ist, unter den nur
ein einziger Gegenstand, nämlich 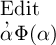 fällt. Da dies nicht nothwendig ist, so kann unsere Festsetzung
in ihrer Allgemeinheit nicht aufrecht erhalten
bleiben.
fällt. Da dies nicht nothwendig ist, so kann unsere Festsetzung
in ihrer Allgemeinheit nicht aufrecht erhalten
bleiben.
Die Gleichung
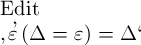 mit
der wir jene Festsetzung versuchten, ist ein besonderer Fall von
mit
der wir jene Festsetzung versuchten, ist ein besonderer Fall von
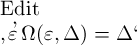 , und
man kann fragen, wie die Function Ω(ξ,
ζ) beschaffen sein müsse, damit allgemein bestimmt werden
dürfe, es solle Δ dasselbe sein wie
, und
man kann fragen, wie die Function Ω(ξ,
ζ) beschaffen sein müsse, damit allgemein bestimmt werden
dürfe, es solle Δ dasselbe sein wie
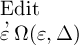 .
Dann muss auch
.
Dann muss auch 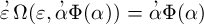
 das Wahre sein, mithin auch
das Wahre sein, mithin auch 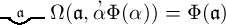
 was auch Φ(ξ) für eine Function sei. Eine Function von
dieser Eigenschaft werden wir später in ξ◠ζ
kennen lernen; aber wir werden sie mit Hilfe des Werthverlaufs
definiren, sodass sie uns hier nichts nützen kann.
was auch Φ(ξ) für eine Function sei. Eine Function von
dieser Eigenschaft werden wir später in ξ◠ζ
kennen lernen; aber wir werden sie mit Hilfe des Werthverlaufs
definiren, sodass sie uns hier nichts nützen kann.
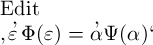
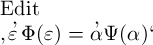 als gleichbedeutend mit
als gleichbedeutend mit 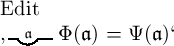 hingestellt haben, ist freilich die Bedeutung eines Namens wie
hingestellt haben, ist freilich die Bedeutung eines Namens wie
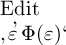 noch
keineswegs vollständig festgestellt. Wir haben nur ein Mittel,
einen Werthverlauf immer wiederzuerkennen, wenn er durch einen
Namen wie
noch
keineswegs vollständig festgestellt. Wir haben nur ein Mittel,
einen Werthverlauf immer wiederzuerkennen, wenn er durch einen
Namen wie 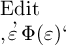 bezeichnet ist, durch welchen er schon als Werthverlauf erkennbar
ist. Aber weder können wir bis jetzt entscheiden, ob ein
Gegenstand, der uns nicht als solcher gegeben ist, ein
Werthverlauf sei, und welcher Function er etwa zugehöre, noch
können wir im Allgemeinen entscheiden, ob ein gegebener
Werthverlauf eine gegebene Eigenschaft habe, wenn wir nicht
wissen, dass diese Eigenschaft verbunden sei mit einer
Eigenschaft der zugehörigen Function. Nehmen wir an, es sei
bezeichnet ist, durch welchen er schon als Werthverlauf erkennbar
ist. Aber weder können wir bis jetzt entscheiden, ob ein
Gegenstand, der uns nicht als solcher gegeben ist, ein
Werthverlauf sei, und welcher Function er etwa zugehöre, noch
können wir im Allgemeinen entscheiden, ob ein gegebener
Werthverlauf eine gegebene Eigenschaft habe, wenn wir nicht
wissen, dass diese Eigenschaft verbunden sei mit einer
Eigenschaft der zugehörigen Function. Nehmen wir an, es sei
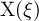
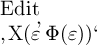 haben, ganz dasselbe Kennzeichen zur Wiedererkennung wie für die
Gegenstände, deren Zeichen die Form
haben, ganz dasselbe Kennzeichen zur Wiedererkennung wie für die
Gegenstände, deren Zeichen die Form 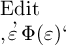 haben. Es ist dann nämlich auch
haben. Es ist dann nämlich auch 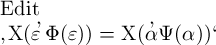 gleichbedeutend mit
gleichbedeutend mit 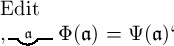 1.
Hieraus geht hervor, dass durch die Gleichsetzung der Bedeutung
von
1.
Hieraus geht hervor, dass durch die Gleichsetzung der Bedeutung
von 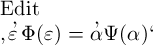 mit
der von
mit
der von 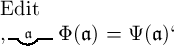 die Bedeutung eines Namens wie
die Bedeutung eines Namens wie 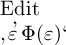 keineswegs völlig bestimmt ist, wenigstens, wenn es eine solche
Function Χ(ξ) giebt, deren Werth
für einen Werthverlauf als Argument diesem selbst nicht immer
gleich ist. Wie wird nun diese Unbestimmtheit aufgehoben?
Dadurch, dass für jede Function bei ihrer Einführung bestimmt
wird, welche Werthe sie für Werthverläufe als Argumente erhält,
ebenso wie für alle andern Argumente. Thun wir dies für die
bisher betrachteten Functionen! Es sind folgende:
keineswegs völlig bestimmt ist, wenigstens, wenn es eine solche
Function Χ(ξ) giebt, deren Werth
für einen Werthverlauf als Argument diesem selbst nicht immer
gleich ist. Wie wird nun diese Unbestimmtheit aufgehoben?
Dadurch, dass für jede Function bei ihrer Einführung bestimmt
wird, welche Werthe sie für Werthverläufe als Argumente erhält,
ebenso wie für alle andern Argumente. Thun wir dies für die
bisher betrachteten Functionen! Es sind folgende:
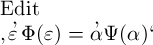 dieselbe Bedeutung haben soll wie
dieselbe Bedeutung haben soll wie 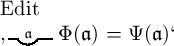 . Es
ist möglich, allgemein festzusetzen, dass
. Es
ist möglich, allgemein festzusetzen, dass 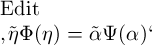 dasselbe bedeuten solle wie
dasselbe bedeuten solle wie 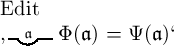 ,
ohne dass daraus die Gleichheit von
,
ohne dass daraus die Gleichheit von 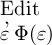 und
und
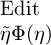 erschlossen werden kann. Wir hätten dann etwa eine Klasse von
Gegenständen, die Namen von der Form
erschlossen werden kann. Wir hätten dann etwa eine Klasse von
Gegenständen, die Namen von der Form 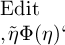 hätten und für deren Unterscheidung und Wiedererkennung dasselbe
Kennzeichen gälte wie für die Werthverläufe. Wir könnten nun die
Function Χ(ξ) dadurch bestimmen,
dass wir sagten, ihr Werth solle das Wahre sein für
hätten und für deren Unterscheidung und Wiedererkennung dasselbe
Kennzeichen gälte wie für die Werthverläufe. Wir könnten nun die
Function Χ(ξ) dadurch bestimmen,
dass wir sagten, ihr Werth solle das Wahre sein für 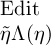 als
Argument und er solle
als
Argument und er solle 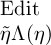 sein für das Wahre als Argument; der Werth der Function
Χ(ξ) solle ferner das Falsche sein
für das Argument
sein für das Wahre als Argument; der Werth der Function
Χ(ξ) solle ferner das Falsche sein
für das Argument 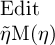 und er solle
und er solle 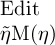 sein für das Falsche als Argument; für jedes andere Argument
solle der Werth der Function Χ(ξ)
Korrektur innerhalb des
Formelteils: funcarg [Rev.: thiel]# mit diesem
selbst zusammenfallen. Wenn nun die Functionen Λ(ξ) und Μ(ξ)
nicht immer für dasselbe Argument denselben Werth haben, so hat
unsere Function Χ(ξ) für
verschiedene Argumente nie denselben Werth, und daher ist dann
auch
sein für das Falsche als Argument; für jedes andere Argument
solle der Werth der Function Χ(ξ)
Korrektur innerhalb des
Formelteils: funcarg [Rev.: thiel]# mit diesem
selbst zusammenfallen. Wenn nun die Functionen Λ(ξ) und Μ(ξ)
nicht immer für dasselbe Argument denselben Werth haben, so hat
unsere Function Χ(ξ) für
verschiedene Argumente nie denselben Werth, und daher ist dann
auch 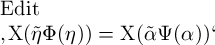 immer gleichbedeutend mit
immer gleichbedeutend mit 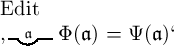 .
Die Gegenstände, deren Namen die Form
.
Die Gegenstände, deren Namen die Form 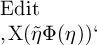 hätten, würden dann also durch dasselbe Mittel wiedererkannt wie
die Werthverläufe, und es wäre
hätten, würden dann also durch dasselbe Mittel wiedererkannt wie
die Werthverläufe, und es wäre 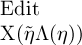 das Wahre und
das Wahre und 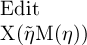 das Falsche. Ohne also mit der Gleichsetzung von
das Falsche. Ohne also mit der Gleichsetzung von 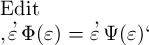 mit
mit
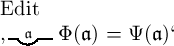 in
Widerspruch zu gerathen, ist es immer möglich zu bestimmen, dass
ein beliebiger Werthverlauf das Wahre und ein beliebiger anderer
das Falsche sein solle. Setzen wir demnach fest, dass
in
Widerspruch zu gerathen, ist es immer möglich zu bestimmen, dass
ein beliebiger Werthverlauf das Wahre und ein beliebiger anderer
das Falsche sein solle. Setzen wir demnach fest, dass
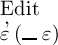 das
Wahre und dass
das
Wahre und dass  das Falsche sein solle!
das Falsche sein solle! 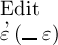 ist der Werthverlauf der Function —ξ, deren Werth nur dann das Wahre ist, wenn
das Argument das Wahre ist, und deren Werth für alle andern
Argumente das Falsche ist. Alle Functionen, von denen dies gilt,
haben
ist der Werthverlauf der Function —ξ, deren Werth nur dann das Wahre ist, wenn
das Argument das Wahre ist, und deren Werth für alle andern
Argumente das Falsche ist. Alle Functionen, von denen dies gilt,
haben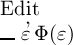 nur dann das Wahre, wenn die Function Φ(ξ) ein Begriff ist, unter den nur das Wahre
fällt; in allen andern Fällen ist
nur dann das Wahre, wenn die Function Φ(ξ) ein Begriff ist, unter den nur das Wahre
fällt; in allen andern Fällen ist 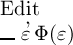 das
Falsche. Ferner ist
das
Falsche. Ferner ist  der Werthverlauf der Function
der Werthverlauf der Function  ,
deren Werth nur dann das Wahre ist, wenn das Argument das Falsche
ist, und deren Werth für alle andern Argumente das Falsche ist.
Alle Functionen, von denen dies gilt, haben denselben
Werthverlauf, und dieser ist nach unserer Festsetzung das
Falsche. Jeder Begriff also, unter den das Falsche und nur dieses
fällt, hat als Begriffsumfang das Falsche1. Wir
haben hiermit die Werthverläufe so
weit bestimmt, als es hier möglich ist. Erst wenn es sich ferner
darum handeln sollte, eine Function einzuführen, welche auf die
bisher bekannten Functionen nicht ganz zurückführbar ist, können
wir festsetzen, welche Werthe sie für Werthverläufe als Argumente
haben solle; und dies kann dann ebenso wohl als eine Bestimmung
der Werthverläufe wie jener Function angesehen werden.
,
deren Werth nur dann das Wahre ist, wenn das Argument das Falsche
ist, und deren Werth für alle andern Argumente das Falsche ist.
Alle Functionen, von denen dies gilt, haben denselben
Werthverlauf, und dieser ist nach unserer Festsetzung das
Falsche. Jeder Begriff also, unter den das Falsche und nur dieses
fällt, hat als Begriffsumfang das Falsche1. Wir
haben hiermit die Werthverläufe so
weit bestimmt, als es hier möglich ist. Erst wenn es sich ferner
darum handeln sollte, eine Function einzuführen, welche auf die
bisher bekannten Functionen nicht ganz zurückführbar ist, können
wir festsetzen, welche Werthe sie für Werthverläufe als Argumente
haben solle; und dies kann dann ebenso wohl als eine Bestimmung
der Werthverläufe wie jener Function angesehen werden.
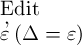 dasselbe wie Δ. Eine solche ist für
jeden Gegenstand möglich, der uns unabhängig von Werthverläufen
gegeben ist, aus demselben Grunde, den wir bei den
Wahrheitswerthen gesehen haben. Aber ehe wir diese Festsetzung
allgemein machen dürfen, fragt es sich, ob sie nicht in
Widerspruch mit unserm Wiedererkennungszeichen der Werthverläufe
stehe, wenn wir für Δ einen
Gegenstand nehmen, der uns schon als Werthverlauf gegeben ist. Es
geht nämlich nicht an, sie nur für solche Gegenstände gelten zu
lassen, welche uns nicht als Werthverläufe gegeben sind, weil die
Weise wie ein Gegenstand gegeben ist, nicht als dessen
unveränderliche Eigenschaft angesehen werden darf, sintemal
derselbe Gegenstand in verschiedener Weise gegeben werden kann.
Setzen wir also für ‚Δ‘
dasselbe wie Δ. Eine solche ist für
jeden Gegenstand möglich, der uns unabhängig von Werthverläufen
gegeben ist, aus demselben Grunde, den wir bei den
Wahrheitswerthen gesehen haben. Aber ehe wir diese Festsetzung
allgemein machen dürfen, fragt es sich, ob sie nicht in
Widerspruch mit unserm Wiedererkennungszeichen der Werthverläufe
stehe, wenn wir für Δ einen
Gegenstand nehmen, der uns schon als Werthverlauf gegeben ist. Es
geht nämlich nicht an, sie nur für solche Gegenstände gelten zu
lassen, welche uns nicht als Werthverläufe gegeben sind, weil die
Weise wie ein Gegenstand gegeben ist, nicht als dessen
unveränderliche Eigenschaft angesehen werden darf, sintemal
derselbe Gegenstand in verschiedener Weise gegeben werden kann.
Setzen wir also für ‚Δ‘
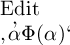 ein,
so erhalten wir
ein,
so erhalten wir 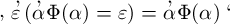
![]() und dies wäre gleichbedeutend mit
und dies wäre gleichbedeutend mit
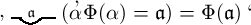
![]() was aber nur dann das Wahre bedeutet, wenn
Φ(ξ) ein Begriff ist, unter den nur
ein einziger Gegenstand, nämlich
was aber nur dann das Wahre bedeutet, wenn
Φ(ξ) ein Begriff ist, unter den nur
ein einziger Gegenstand, nämlich 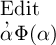 fällt. Da dies nicht nothwendig ist, so kann unsere Festsetzung
in ihrer Allgemeinheit nicht aufrecht erhalten
bleiben.
fällt. Da dies nicht nothwendig ist, so kann unsere Festsetzung
in ihrer Allgemeinheit nicht aufrecht erhalten
bleiben.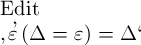 mit
der wir jene Festsetzung versuchten, ist ein besonderer Fall von
mit
der wir jene Festsetzung versuchten, ist ein besonderer Fall von
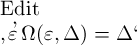 , und
man kann fragen, wie die Function Ω(ξ,
ζ) beschaffen sein müsse, damit allgemein bestimmt werden
dürfe, es solle Δ dasselbe sein wie
, und
man kann fragen, wie die Function Ω(ξ,
ζ) beschaffen sein müsse, damit allgemein bestimmt werden
dürfe, es solle Δ dasselbe sein wie
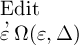 .
Dann muss auch
.
Dann muss auch